|
Jean Debord
JDebord@compuserve.com ou jdebord@MicroNet.fr
http://ourworld.compuserve.com/homepages/JDebord/
|
I. ThéorieI.A. DéfinitionsUne matrice n × m est un tableau de nombres à n lignes et m colonnes :
Une matrice est symbolisée par une lettre en caractères gras, par exemple A. On note Aij l'élément situé à l'intersection de la ligne i et de la colonne j (la ligne est toujours nommée en premier).  On note [Aij] la matrice d'élément général Aij. On a donc : A = [Aij] Si m = 1, la matrice est appelée vecteur (plus précisément vecteur-colonne) : 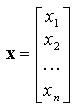 N.B. : Dans ce chapitre, nous utiliserons des lettres majuscules pour les matrices et des lettres minuscules pour les vecteurs, mais ce n'est pas obligatoire. Si n = m, la matrice est appelée matrice carrée. Quelques matrices carrées particulières (Exemples avec n = 4)
I.B. Opérations sur les matricesI.B.1. Addition, soustractionL'addition et la soustraction des matrices se font terme à terme. Les matrices doivent avoir les mêmes dimensions :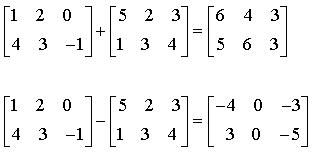 I.B.2. Multiplication par un nombreChaque terme de la matrice est multiplié par le nombre :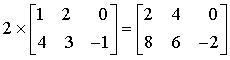 I.B.3. TranspositionLa transposée AT (aussi notée A') d'une matrice A est la matrice obtenue en échangeant les lignes et les colonnes de A :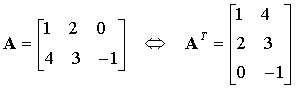 La transposée d'un vecteur-colonne est un vecteur-ligne : 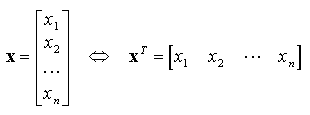 I.B.4. Multiplication des matricesDéfinissons tout d'abord le produit d'un vecteur-ligne xT par un vecteur-colonne y : 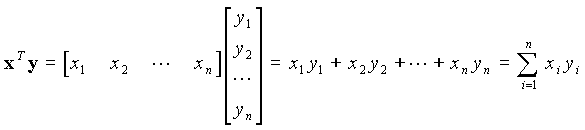 Ce produit est appelé produit scalaire des vecteurs x et y, noté x · y. Les vecteurs doivent avoir la même dimension. Le produit matriciel s'en déduit : le produit de la matrice A (n × m) par la matrice B (m × p) est la matrice C (n × p) telle que l'élément Cij est égal au produit scalaire de la ligne i de la matrice A par la colonne j de la matrice B. 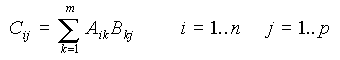 Exemple : 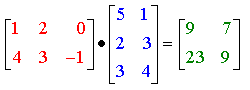 On a en effet, en effectuant les produits ligne par colonne : 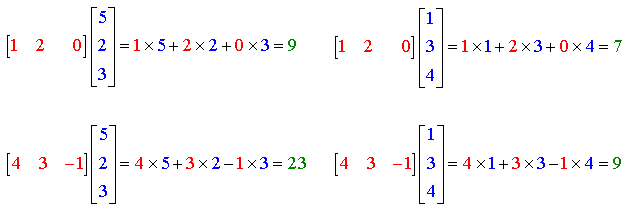 Propriétés :
La matrice unité I est élément neutre pour la multiplication : AIm = InA = A, si la matrice A est de dimensions n × m. Transposée d'un produit : (AB)T = BTAT (Attention au changement d'ordre !). Quelques produits particuliers : (x et y sont des vecteurs-colonnes, A est une matrice)
I.B.5. Inversion des matrices carréesUne matrice carrée A est dite inversible ou régulière s'il existe une matrice carrée A-1 (appelée matrice inverse) telle que :Si A-1 n'existe pas, la matrice A est dite singulière Propriétés :
(AT)-1 = (A-1)T (AB)-1 = B-1A-1 (Attention au changement d'ordre !) [diag(Dii)]-1 = diag(1/Dii) La matrice A est dite orthogonale si A-1 = AT I.B.6. Déterminant d'une matrice carréePour une matrice 2 × 2, on montre que la matrice inverse est donnée par :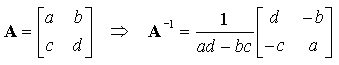 Le nombre ad - bc est appelé déterminant de la matrice A, noté : 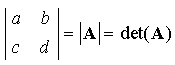 La matrice inverse A-1 n'existe donc que si det A est différent de zéro. La matrice A est singulière si det A = 0, régulière dans le cas contraire. Ce résultat se généralise à une matrice de dimension quelconque. Le déterminant peut se calculer de manière récursive. Par exemple, pour n = 3, on a , en développant par rapport à la première ligne : 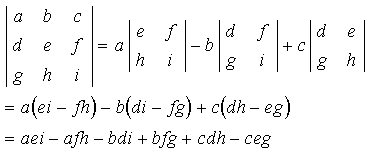 Dans ce développement, chaque déterminant d'ordre 2 est appelé mineur du terme qui le précède. Par exemple, le mineur de a est : 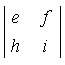 On peut développer le déterminant par rapport à n'importe quelle ligne ou colonne. Pour chaque élément aij de la ligne ou colonne choisie : Cette méthode est valable pour un déterminant de taille quelconque. En fait pour n > 3, il vaut mieux utiliser un algorithme spécifique tel que l'algorithme de décomposition LU. Propriétés des déterminants :
det(AB) = det(A) × det(B) Le déterminant d'une matrice triangulaire ou diagonale est égal au produit des éléments diagonaux. En particulier, det(I) = 1 (si I est la matrice unité) Si A est régulière, det(A-1)
= 1 / det(A)
Si A est orthogonale, det(A) = ±1
I.C. Application aux systèmes d'équations linéairesI.C.1. Formulation matricielleUn système de n équations linéaires à n inconnues est de la forme :où les aij sont les coefficients du système, les xi les inconnues et les bi les termes constants. Un tel système peut s'écrire sous forme matricielle : avec : 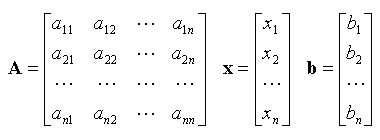 I.C.2. Cas d'une matrice régulièreSi la matrice A est régulière, on a, en multipliant à gauche par A-1 :Soit : Exemple : Soit le système de 2 équations à 2 inconnues : On a successivement : 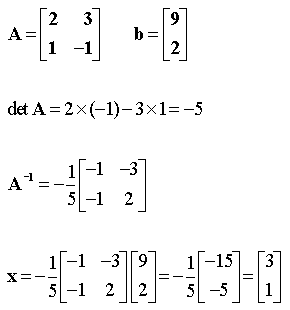 I.C.3. Cas d'une matrice singulièreLorsque la matrice est singulière, deux cas sont à envisager :S'il est possible d'exprimer p équations en fonction des autres, le système admet une infinité de solutions. On peut retenir le vecteur x qui a la plus faible norme. L'ensemble des solutions forme un sous-espace de dimension r = n - p dans l'espace de dimension n. Le nombre r est le rang de la matrice. Exemple : Le déterminant vaut : 1 × 2 - 1 × 2 = 0. La matrice est bien singulière. La deuxième équation est égale à la première multipliée par 2. Il n'y a en fait qu'une seule équation : x1 + x2 = 3. C'est l'équation d'une droite (espace de dimension 1) dans le plan (x1, x2). La matrice est de rang 1. Si les équations ne peuvent pas être exprimées les unes en fonction des autres, le système n'admet aucune solution. On peut cependant calculer un vecteur x tel que la norme du vecteur Ax - b soit minimale (bien que non nulle). Ce vecteur constitue la meilleure approximation de la solution au sens des moindres carrés (voir le cours sur la régression linéaire). Exemple : La deuxième équation divisée par 2 donnerait x1 + x2 = 4, ce qui est incompatible avec la première équation. Le système n'a pas de solution. I.D. Résolution des systèmes d'équations linéairesLes principales méthodes de résolution des systèmes d'équations linéaires sont les suivantes :I.D.1. Méthode de Gauss-JordanLa méthode de Gauss-Jordan calcule simultanément la matrice inverse A-1 et le vecteur solution x. S'il y a plusieurs systèmes à résoudre, on peut réunir tous les vecteurs de termes constants bi dans une matrice unique B (chaque vecteur constituant une colonne de la matrice). L'application de l'algorithme de Gauss-Jordan fournit alors une matrice X dont la colonne i constitue la solution du ième système.Cette méthode exige que tous les vecteurs de termes constants
soient connus au moment d'appliquer l'algorithme. Si tel n'est pas le cas,
ou si la matrice inverse n'est pas requise, il vaut mieux choisir la méthode
LU qui est plus rapide.
I.D.2. Décomposition LUCette méthode exprime la matrice A sous forme du produit d'une matrice triangulaire inférieure L à diagonale unité par une matrice triangulaire supérieure U :Exemple avec n = 4 : 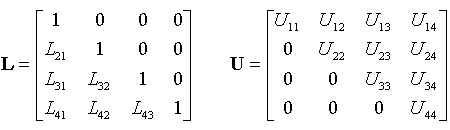 Le système devient : soit : On résout le système (1) pour trouver le vecteur y, puis le système (2) pour trouver le vecteur x. La résolution est facilitée par la forme triangulaire des matrices. La méthode LU permet aussi de calculer le déterminant
de A, qui est égal au produit des éléments
diagonaux de la matrice U, puisque det(A) = det(L)
× det(U) et det(L) = 1 (Rappelons que le déterminant
d'une matrice triangulaire est égal au produit de ses éléments
diagonaux).
I.D.3. Décomposition en valeurs singulièresLa décomposition en valeurs singulières (SVD, Singular Value Decomposition) exprime la matrice A sous la forme :U et V sont des matrices orthogonales. S est une matrice diagonale. Ses termes diagonaux Sii, tous positifs ou nuls, sont les valeurs singulières de A. Le rang de A est égal au nombre de valeurs singulières non nulles. (en se rappelant que l'inverse d'une matrice orthogonale est égale à sa transposée) On en déduit la solution du système par x = A-1b On montre que la solution ainsi calculée correspond : I.D.4. Méthode de CholeskyUne matrice symétrique A est dite définie positive si, pour tout vecteur x, le produit xTAx est positif (Exemple en régression linéaire : les matrices de variance-covariance ou les matrices des équations normales).Pour une telle matrice, on montre qu'il est possible de trouver une matrice triangulaire inférieure L telle que : L peut être considérée comme une sorte de "racine carrée" de A. Cette décomposition permet de : II. Programmation en Turbo PascalLa programmation des calculs précédents peut être réalisée au moyen de la bibliothèque TP MATH.II.A. L'unité MATRICES.PASL'unité MATRICES.PAS, contenue dans TPMATH1.ZIP fournit les fonctions de calcul matriciel décrites dans ce chapitre.II.A.1. Représentation des vecteurs et matricesAfin de permettre l'allocation dynamique des tableaux, les vecteurs et matrices sont représentés par des pointeurs. Il y a 8 types disponibles :
II.A.2. Règles d'utilisation des vecteurs et matrices
var V : PVector; A : PMatrix;Allouer chaque tableau AVANT de l'utiliser : DimVector(V, N); { crée le vecteur V de dimension N }
DimMatrix(A, N, M); { crée la matrice A de dimensions N × M }
{ où N, M sont des variables entières }
La dimension maximale des vecteurs est fonction du type de variable qu'ils
contiennent. Elle est fixée par les constantes suivantes :
const
MAX_FLT = 6552; { Type Extended (10921 en type Real) }
MAX_INT = 32766; { Type entier }
MAX_BOOL = 65534; { Type booléen }
MAX_STR = 254; { Type chaîne de caractères }
Les dimensions maximales d'une matrice sont :
DimVector(V, N);
if V = nil then
Write('Pas assez de mémoire !');
Remarque : Cette étape d'allocation de mémoire est
capitale. Si les tableaux ne sont pas correctement alloués, la lecture
et l'écriture des éléments se fait n'importe où,
provoquant des dysfonctionnements du programme pouvant aller jusqu'au blocage
de l'ordinateur. Ici le Pascal devient aussi dangereux que le C !
On accède aux éléments d'un tableau comme en Turbo Pascal standard, avec toutefois deux exceptions : V^[I] { au lieu de V[I] }
A^[I]^[J] { au lieu de A[I,J] }
Ces notations dérivent du fait que les vecteurs et matrices sont
représentés par des pointeurs. C'est un peu lourd, mais c'est
le prix à payer pour avoir l'allocation dynamique, qui fait cruellement
défaut au Turbo Pascal (le Basic est mieux pourvu sur ce plan).
Une matrice est déclarée comme un tableau de vecteurs, chaque vecteur représentant une ligne de la matrice. A^[I] désigne donc le Ième vecteur (la Ième ligne) de la matrice A, et peut être manipulé comme n'importe quel vecteur. Dans les fonctions ou procédures, les paramètres de type vecteur ou matrice doivent être passés avec l'attribut var lorsque les tableaux sont dimensionnés à l'intérieur de la procédure. Dans le cas contraire, cet attribut n'est pas nécessaire. DelVector(V, N); DelMatrix(A, N, M); II.A.3. Conventions de programmationLes conventions suivantes ont été adoptées pour les procédures de l'unité MATRICES :
II.A.4. Procédures d'allocation de mémoireIl y a 8 procédures d'allocation de mémoire, une pour chacun des types précédemment définis. Notez que le paramètre vecteur ou matrice possède l'attribut var car le tableau est dimensionné à l'intérieur de la procédure.
II.A.5. Procédures de libération de la mémoireChaque procédure Dim... a sa contrepartie sous forme d'une procédure Del... qui libère la mémoire occupée par le tableau. Ici l'attribut var n'est pas nécessaire car le tableau est déjà dimensionné.
II.A.6. Copie de vecteurs et matricesLes procédures suivantes sont disponibles :
Echange les lignes I et K de la matrice A. Echange les colonnes J et K de la matrice A. Copie le vecteur Source dans le vecteur Dest. Copie la matrice Source dans la matrice Dest. Copie le vecteur Source dans la ligne Row de la matrice Dest. Copie le vecteur Source dans la colonne Col de la matrice Dest. Copie la ligne Row de la matrice Source dans le vecteur Dest. Copie la colonne Col de la matrice Source dans le vecteur Dest. II.A.7. Minimum et maximum d'un vecteurLes fonctions suivantes sont disponibles :
II.A.8. Transposition de matriceLa procédure suivante transpose la matrice A et retourne le résultat dans A_t :procedure Transpose(A : PMatrix; Lbound1, Lbound2, Ubound1, Ubound2 : Integer; A_t : PMatrix); II.A.9. Déterminant d'une matrice carréeLa fonction suivante retourne le déterminant de la matrice A. La matrice est détruite durant l'opération :function Det(A : PMatrix; Lbound, Ubound : Integer) : Float; II.A.10. Systèmes linéairesPlusieurs fonctions et procédures permettent de résoudre les systèmes d'équations linéaires par les différentes méthodes que nous avons vues. Chaque fonction retourne un code d'erreur parmi les suivants :----------------------------------------------------------------- Symbole Valeur Signification Retourné par ----------------------------------------------------------------- MAT_OK 0 Pas d'erreur Toute fonction MAT_SINGUL -1 Matrice singulière GaussJordan InvMat LU_Decomp (*) MAT_NON_CONV -2 Non-convergence SV_Decomp (*) MAT_NOT_PD -3 Matrice non définie positive Cholesky (*) Ces fonctions détruisent la matrice d'origine -----------------------------------------------------------------Ces fonctions et procédures sont les suivantes :
Résout le système AX = B par la méthode de Gauss-Jordan. La matrice inverse est retournée dans A_inv Calcule la matrice inverse par la méthode de Gauss-Jordan. Effectue la décomposition LU. Les éléments des matrices L et U sont stockés dans A, qui est donc détruite. Résout le système AX = B par la méthode LU, une fois que la matrice A a été transformée par LU_Decomp. Effectue la décomposition en valeurs singulières, A = USV' ; A est une matrice (n × m) avec n >= m. La matrice U est stockée dans A, qui est donc détruite. Met à zéro les valeurs singulières inférieures à Tol. Résout le système USV'X = B, après décomposition en valeurs singulières par SV_Decomp, et mise à zéro des plus faibles valeurs singulières par SV_SetZero. Calcule la décomposition de Cholesky, A = LLT ; A est symétrique définie positive. II.B. Programmes de démonstrationLes programmes suivants sont disponibles dans TPMATH2.ZIP :
II.B.1. Déterminant et inverse d'une matrice carréeLe programme DETINV.PAS calcule le déterminant et inverse d'une matrice carrée. La matrice est lue dans un fichier ASCII dont la structure est la suivante :
La procédure ReadMatrix lit le fichier de données. Notez que la matrice est dimensionnée à l'intérieur de la procédure, d'où l'attribut var. procedure ReadMatrix(FileName : String; var A : PMatrix;
var N : Integer);
var
F : Text; { Fichier de données }
I, J : Integer; { Variables de boucle }
begin
Assign(F, FileName);
Reset(F);
Read(F, N);
DimMatrix(A, N, N);
for I := 1 to N do
for J := 1 to N do
Read(F, A^[I]^[J]);
Close(F);
end;
On calcule ensuite la matrice inverse puis le déterminant
(dont le calcul détruit la matrice d'origine). La matrice inverse
est ensuite réinversée pour vérifier que l'on retrouve
bien la matrice d'origine.
case InvMat(A, 1, N, A_inv) of
MAT_OK : begin
D := Det(A, 1, N);
{ Ecrire le déterminant et la matrice inverse }
if InvMat(A_inv, 1, N, A) = MAT_OK then
{ Ecrire la matrice réinversée }
end;
MAT_SINGUL : { Matrice singulière }
end;
Remarque : On a considéré que la
matrice commence à l'indice 1. Si la matrice commençait à
l'indice 0, il faudrait écrire InvMat(A,
0, N, A_inv) etc.
Les résultats obtenus avec le fichier MATRIX1.DAT sont les suivants : Original matrix : 1.000000 2.000000 0.000000 -1.000000 -1.000000 4.000000 3.000000 -0.500000 2.000000 2.000000 1.000000 -3.000000 0.000000 0.000000 3.000000 -4.000000 Inverse matrix : -1.952381 0.190476 1.571429 -0.714286 0.761905 0.047619 -0.357143 0.071429 -1.904762 0.380952 1.142857 -0.428571 -1.428571 0.285714 0.857143 -0.571429 Determinant = -21.000000 Reinverted inverse matrix : 1.000000 2.000000 0.000000 -1.000000 -1.000000 4.000000 3.000000 -0.500000 2.000000 2.000000 1.000000 -3.000000 0.000000 -0.000000 3.000000 -4.000000 II.B.2. Méthode de Gauss-JordanLe programme SYSEQ.PAS teste la méthode de Gauss-Jordan en résolvant une série de systèmes de Hilbert d'ordre croissant. La matrice d'un tel système est de la forme :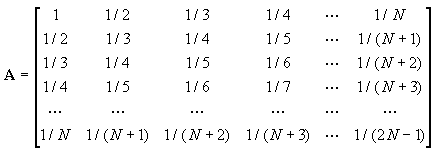 Chaque élément du vecteur de termes constants B est égal à la somme des termes de la ligne correspondante de la matrice : 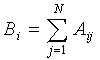 La solution d'un tel système est : Le programme principal a la forme suivante. Noter le redimensionnement des tableaux à chaque tour de boucle. N := 1;
ErrCode := 0;
while ErrCode = 0 do
begin
{ Définir l'ordre du système }
Inc(N);
{ Allouer vecteurs et matrices }
DimMatrix(A, N, N);
DimVector(B, N);
DimMatrix(A_inv, N, N);
DimVector(X, N);
{ Générer le système de Hilbert d'ordre N
--> Matrice A et vecteur B }
{ Résoudre le système }
ErrCode := GaussJordan(A, B, 1, N, A_inv, X);
{ Ecrire la solution }
{ Désallouer les tableaux pour qu'ils puissent
être redimensionnés à l'itération suivante }
DelMatrix(A, N, N);
DelVector(B, N);
DelMatrix(A_inv, N, N);
DelVector(X, N);
end;
II.B.3. Décompositions LU et SVDLes programmes SYSEQLU.PAS et SYSEQSVD.PAS résolvent une série de systèmes linéaires ayant même matrice mais différents vecteurs de termes constants, en utilisant la décomposition LU ou la décomposition en valeurs singulières. Les données sont lues dans un fichier ASCII dont la structure est la suivante :
La procédure ReadMatrices lit le fichier de données. Les vecteurs constants sont stockés dans une matrice B, chaque vecteur constituant une ligne de la matrice, de sorte que B^[I] représente le Ième vecteur constant. La matrice B est donc la transposée de celle qui est stockée dans le fichier. procedure ReadMatrices(FileName : String; var A, B : PMatrix;
var N, P : Integer);
var
F : Text; { Fichier de données }
I, J : Integer; { Variables de boucle }
begin
Assign(F, FileName);
Reset(F);
{ Lire la matrice des coefficients }
Read(F, N);
DimMatrix(A, N, N);
for I := 1 to N do
for J := 1 to N do
Read(F, A^[I]^[J]);
{ Lire les vecteurs constants dans une matrice B,
transposée de celle qui est dans le fichier }
Read(F, P);
DimMatrix(B, P, N);
for J := 1 to N do
for I := 1 to P do
Read(F, B^[I]^[J]);
Close(F);
end;
La matrice A est ensuite décomposée, puis
la procédure de résolution est appliquée à
chacun des vecteurs constants. Pour la décomposition LU cela donne
:
{ Décomposition LU. Les matrices L et U sont stockées dans A }
case LU_Decomp(A, 1, N) of
MAT_OK : begin
{ Résoudre le système pour chaque vecteur constant }
for I := 1 to P do
LU_Solve(A, B^[I], 1, N, X^[I]);
{ Ecrire la solution }
end;
MAT_SINGUL : { Matrice singulière }
end;
Pour la décomposition SVD, la matrice est considérée
comme singulière lorsque certaines valeurs singulières sont
inférieures à une certaine fraction de la plus grande. Cette
fraction est représentée dans le programme par la constante
TOL, fixée arbitrairement à 10-8. Ces valeurs
doivent être obligatoirement mises à zéro avant d'appeler
la procédure de résolution. L'algorithme est donc le suivant
:
{ Décomposition SVD. La matrice U est stockée dans A }
case SV_Decomp(A, 1, N, N, S, V) of
MAT_OK : begin
{ Mise à zéro des plus faibles valeurs singulières }
SV_SetZero(S, 1, N, TOL);
{ Résoudre le système pour chaque vecteur constant }
for I := 1 to P do
SV_Solve(A, S, V, B^[I], 1, N, N, X^[I]);
{ Ecrire la solution }
end;
MAT_NON_CONV : { Non-convergence }
end;
Avec le fichier MATRIX2.DAT les deux programmes donnent
les mêmes résultats :
System matrix : 2.000000 1.000000 5.000000 -8.000000 7.000000 6.000000 2.000000 2.000000 -1.000000 -3.000000 -10.000000 4.000000 2.000000 2.000000 2.000000 1.000000 Constant vectors : 0.000000 -15.000000 14.000000 -13.000000 5.000000 17.000000 50.000000 1.000000 84.000000 30.000000 -10.000000 -5.000000 -12.000000 -51.000000 -15.000000 7.000000 17.000000 1.000000 37.000000 10.000000 Solution vectors : 1.000000 2.000000 1.000000 4.000000 0.000000 1.000000 5.000000 -1.000000 5.000000 5.000000 1.000000 0.000000 1.000000 6.000000 0.000000 1.000000 3.000000 -1.000000 7.000000 0.000000 II.B.4. Décomposition de CholeskyLe programme CHOLESK.PAS calcule la décomposition de Cholesky d'une matrice symétrique définie positive. La matrice est lue dans un fichier ASCII (comme pour DETINV.PAS). Le fichier MATRIX4.DAT est un exemple avec N = 3.Après lecture des données, la matrice est décomposée puis on calcule le produit LLT qui doit redonner la matrice de départ : case Cholesky(A, 1, N, L) of
MAT_OK : { Calculer LLT et écrire les résultats }
MAT_NOT_PD : { Matrice non définie positive }
end;
Les résultats obtenus avec le fichier MATRIX4.DAT
sont les suivants :
Original matrix : 60.000000 30.000000 20.000000 30.000000 20.000000 15.000000 20.000000 15.000000 12.000000 Cholesky factor (L) : 7.745967 0.000000 0.000000 3.872983 2.236068 0.000000 2.581989 2.236068 0.577350 Product L * L' : 60.000000 30.000000 20.000000 30.000000 20.000000 15.000000 20.000000 15.000000 12.000000 |